기본적인 자료 구조 중 하나인 Binary Search Tree(이진 탐색 트리)를 Go언어를 이용해 구현해본다.
Definition
Binary search tree(이하 BST)는 각 노드에 값이 있으며 그 값이 특정한 순서로 정렬이 가능할 때, 그 순서에 따라 정렬이 되어 있는 Binary tree를 의미한다. 이 글에서 Binary tree에 대한 정의는 위키피디아 링크로 대체한다.
노드의 순서는 대체로 대상 노드의 왼쪽 자식 트리는 대상 노드의 값보다 작은 값들을 가지며, 오른쪽 자식 트리는 대상 노드의 값보다 큰 값들을 가진다.
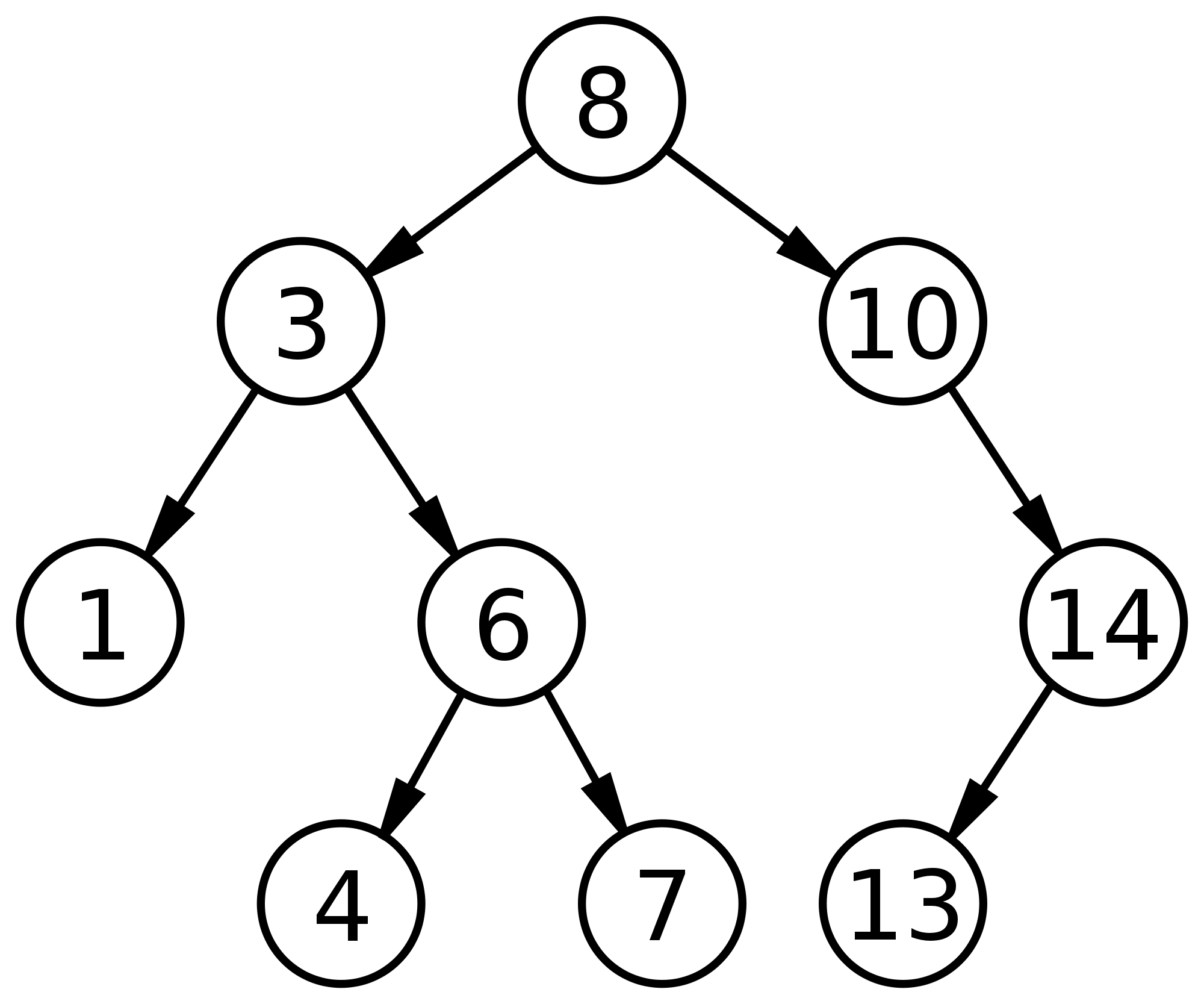
Binary search tree
기초적인 자료 구조를 얘기할 때 빠지지 않고 등장하는 BST는 정렬 및 검색을 효율적으로 할 수 있도록 도와줄 뿐 아니라, 기초적인 자료 구조답게 구현이 쉽다.
Time complexity
BST의 노드 검색은 기본 O(logN)의 시간 복잡도를 가지며, 최악의 시나리오(모든 노드가 한쪽 자식 노드로 치우쳐 있는 경우)에서 O(N)의 시간 복잡도를 가진다.
Operations
위키피디아를 기준으로, BST의 기본적인 기능은 다음과 같다.
- 검색 (Searching)
- 삽입 (Insertion)
- 삭제 (Deletion)
- 순회 (Traversal)
- 검증 (Verification)
Implementation
BST의 각 기능을 구현하기 이전에, 노드 타입을 정의할 필요가 있다.
1 | // Node is a single node in the tree |
2 | type Node struct { |
3 | key int |
4 | value int |
5 | left *Node |
6 | right *Node |
7 | } |
각 노드는 key와 value를 가지며, 2개의 자식 노드를 가리키는 포인터를 가진다. 자식 노드는 left와 right로 구별하였다.
그리고 전체 트리 구조를 파악할 수 있도록 루트 노드를 가리키는 BST 타입을 정의한다.
1 | // Bst is the binary search tree |
2 | type Bst struct { |
3 | root *Node |
4 | } |
Searching
원하는 key를 입력했을 때 해당 키를 갖는 노드를 반환하는 함수를 구현한다.
만약 해당 key를 갖는 노드를 찾을 수 없는 경우 nil을 반환하도록 하였다.
1 | // Search searches the targe node using key from the tree |
2 | func (bst *Bst) Search(key int) *Node { |
3 | return search(bst.root, key) |
4 | } |
5 | |
6 | // search is the internal recursive function to find the node by key |
7 | // it returns nil if no node was found |
8 | func search(n *Node, k int) *Node { |
9 | if n == nil || n.key == k { |
10 | return n |
11 | } |
12 | if k < n.key { |
13 | return search(n.left, k) |
14 | } |
15 | // k > n.key |
16 | return search(n.right, k) |
17 | } |
Insertion
key와 value를 입력으로 받아 대상 트리에 새로운 노드를 추가하는 함수를 구현한다.
만약 트리가 root 노드가 존재하지 않는 빈 트리라면, 새로운 노드를 root 노드로써 추가한다.
1 | // Insert inserts the new node into the tree |
2 | func (bst *Bst) Insert(key int, value Item) { |
3 | n := &Node{key, value, nil, nil} |
4 | if bst.root == nil { |
5 | bst.root = n |
6 | } else { |
7 | insert(bst.root, n) |
8 | } |
9 | } |
만약 트리에 이미 root 노드가 존재하면, 새로운 노드를 추가할 올바른 위치를 찾아야한다.
key를 비교하며 새로운 노드가 추가될 위치를 찾는 재귀함수 insert(n *Node, new *Node)를 구현한다.
1 | // insert is the internal recursive function to insert new node |
2 | // by finding proper position recursively |
3 | func insert(n *Node, new *Node) { |
4 | if new.key < n.key { |
5 | if n.left == nil { |
6 | n.left = new |
7 | } else { |
8 | insert(n.left, new) |
9 | } |
10 | } else { |
11 | if n.right == nil { |
12 | n.right = new |
13 | } else { |
14 | insert(n.right, new) |
15 | } |
16 | } |
17 | } |
Deletion
BST에서 노드의 삭제는 다른 동작들보다 복잡하다. 노드를 삭제한 뒤에도 전체 BST는 BST로써의 기능을 유지해야 한다. 따라서 어떤 노드가 삭제되는가에 따라 BST 형태를 유지하기 위한 추가 처리가 필요할 수 있다. 이해를 쉽게 하기 위해서, 우선 어떤 경우가 있는지 살펴보자.
- 자식 노드를 가지지 않는 leaf 노드를 삭제하는 경우
- 하나의 자식 노드만 가지는 노드를 삭제하는 경우
- 좌/우 자식을 모두 가지는 노드를 삭제하는 경우
먼저, BST에 대한 함수 Delete(k int)와 실제 삭제 처리를 담당할 내부 재귀함수 delete(n *Node, k int)의 기본은 다음과 같다.
1 | func (bst *Bst) Delete(k int) { |
2 | delete(bst.root, k) |
3 | } |
4 | |
5 | func delete(n *Node, k int) *Node { |
6 | // if current node is not the target node |
7 | if n == nil { |
8 | return nil |
9 | } else if k < n.key { |
10 | n.left = remove(n.left, k) |
11 | return n |
12 | } else if k > n.key { |
13 | n.right = remove(n.right, k) |
14 | return n |
15 | } |
16 | |
17 | // if current node is the target node |
18 | ... |
19 | } |
재귀함수 delete(n *Node, k int)에서 현재 노드가 삭제할 노드일 경우에 대한 구현은 아래에서 살펴본다.
1. leaf 노드의 삭제
leaf 노드의 제거는 간단하다.
1 | func delete(n *Node, k int) *Node { |
2 | ... |
3 | if n.left == nil & n.right == nil { |
4 | n = nil |
5 | return nil |
6 | } |
7 | } |
2. 자식을 하나만 가지는 노드의 삭제
위에서 leaf 노드의 경우를 먼저 처리했기 때문에, 하나의 자식 노드가 존재하지 않는 것만 체크하는 것으로 자식을 하나만 가지는 노드를 가릴 수 있다.
대상 노드를 삭제한 뒤에는 대상 노드가 있던 자리를 대상 노드의 자식 노드로 대체하는 것으로 삭제 처리가 완료될 수 있다.
1 | func delete(n *Node, k int) *Node { |
2 | ... |
3 | // if the node has right child only |
4 | if n.left == nil { |
5 | n = n.right |
6 | return n |
7 | } |
8 | // if the node has left child only |
9 | if n.right == nil { |
10 | n = n.left |
11 | return n |
12 | } |
13 | } |
3. 좌/우 자식을 모두 가지는 노드의 삭제
좌/우 자식을 모두 가지는 노드가 삭제된 뒤에는 대상 노드의 자리를 대체할 노드로 어떤 노드를 선택해야할 지 고민할 필요가 있다.
다시 BST의 특성을 떠올려보자.
- 좌측 자식들은 해당 노드보다 작은 키 값을 가진다.
- 우측 자식들은 해당 노드보다 큰 키 값을 가진다.
그렇다면 삭제된 노드를 대체할 수 있는 자식 노드는 다음과 같다.
- 좌측 자식들 중 가장 큰 키 값을 가지는 노드
- 우측 자식들 중 가장 작은 키 값을 가지는 노드
위의 둘 중 어떤 노드로 대체를 하던 상관없겠지만, 번외로써 트리 내의 최대값과 최소값을 찾는 함수를 구현해보자.
1 | // max finds most right child |
2 | func max(n *Node) *Node { |
3 | max := n |
4 | for { |
5 | if max != nil && max.right != nil { |
6 | max = max.right |
7 | } else { |
8 | break |
9 | } |
10 | } |
11 | return max |
12 | } |
13 | |
14 | // min finds most left child |
15 | func min(n *Node) *Node { |
16 | min := n |
17 | for { |
18 | if min != nil && min.left != nil { |
19 | min = min.left |
20 | } else { |
21 | break |
22 | } |
23 | } |
24 | return min |
25 | } |
본 구현에서는 우측 자식들 중 가장 작은 키 값을 가지는 노드로 삭제된 노드를 대체하도록 구현하였다.
현재 노드를 대체한 뒤에는 우측 자식 트리 내에서 대체된 노드를 삭제해야 한다.
1 | func delete(n *Node, k int) *Node { |
2 | n = max(n.right) |
3 | delete(n.right, n.key) |
4 | |
5 | return n |
6 | } |
Traversal
순회는 트리 구조 내의 노드를 순서대로 방문하며 각 아이템을 반환하는 로직이다.
재귀적인 순회 로직을 이용해 왼쪽 서브 트리부터 방문하며, 더 이상의 서브 트리가 존재하지 않는 상황에서 오른쪽 서브 트리에 대해 순회를 반복하는 것으로 순서대로 방문하는 것이 가능하다.
순서대로 방문한 노드에서 반환되는 아이템은 callback 함수를 이용해 프로그래머가 원하는 동작을 할 수 있도록 구현한다.
1 | // Traverse visits all nodes in order |
2 | func (bst *Bst) Traverse(f func(Item)) { |
3 | traverse(bst.root, f) |
4 | } |
5 | |
6 | // traverse is the internal recursive function to visit the nodes |
7 | func traverse(n *Node, f func(Item)) { |
8 | if n != nil { |
9 | traverse(n.left, f) |
10 | f(n.value) |
11 | traverse(n.right, f) |
12 | } |
13 | } |
Verification
이미 Binary tree가 주어진 상황에서, 해당 트리가 BST인지를 검증해야 하는 상황이 있을 수 있다.
BST의 핵심은, 모든 노드를 대상으로 오른쪽 서브 트리는 해당 노드보다 큰 노드만이 존재하며, 왼쪽 서브 트리는 해당 노드보다 작은 노드만이 존재해야 한다는 점이다.
단순히 모든 노드를 순회하며 1개 레벨 아래의 자식 노드와만 비교하는 것으로는 검증을 100% 보장할 수 없다는 점에 주의하자.
1 | // Verify checks the binary tree whether it's BST |
2 | func (bst *Bst) Verify() bool { |
3 | return isBST(bst.root, math.MinInt64, math.MaxInt64) |
4 | } |
5 | |
6 | func isBST(n *Node, min, max int) bool { |
7 | if n == nil { |
8 | return true |
9 | } |
10 | if n.key < min || n.key > max { |
11 | return false |
12 | } |
13 | |
14 | return isBST(n.left, min, n.key-1) && isBST(n.right, n.key+1, max) |
15 | } |
